

Fünf Minuten später saß er mit Emmy auf den harten Zirkusbänken. Die Pferdedressur wurde angekündigt. Zwei glänzende, schwarze Araber trabten majestätisch in die Manege und liefen ein paarmal im Kreis. Sobald die wunderschönen Hengste ihre Plätze in der Mitte der Manege eingenommen hatten, kamen sechzehn weiße Ponys hereingaloppiert. Sie stellten sich im Halbkreis vor die Araber.
Dann knallte die Peitsche. Die Araber bäumten sich auf. Auf den Schmuckbändern
unter ihren Bäuchen wurden zwei knallrote Zahlen sichtbar: 220 und 284.
Dann wurde es auf einen Schlag dunkel, die Ponys teilten sich in zwei Gruppen
und umkreisten die immer noch auf den Hinterbeinen stehenden Araber. Das war
ein Bild: die beiden schwarzen Pferde mit den leuchtend roten Zahlen am Bauch
und in zwei Kreisen um sie herum die kleinen Ponys mit grünen Leuchtzahlen
auf dem Rücken.
Wieder knallte die Peitsche, die Ponys formten eine Acht, und teilten sich abermals
in zwei Gruppen, aber diesmal umkreisten sie genau den anderen Araber. Noch ein
Peitschenknall und unversehens war die Manege wieder leer.
Max genoss den Rest der Vorstellung und kaum hatten sie das Zirkuszelt verlassen,
entfuhr es Emmy:
"Hey, die zwei Araber waren befreundet!"
"Welche Araber, wovon sprichst du?"
"Na die Pferde. Und die Ponys waren ihre Teiler!"
"Also Emmy, mal ganz langsam. Woher willst du denn wissen, ob die Pferde
sich leiden konnten? Und wie können Ponys Teiler von Arabern sein?"
"Der eine Hengst hatte die 284. Um ihn sind die 1, 2, 4, 71 und die 142
gelaufen. Das sind genau die Zahlen, durch die 284 teilbar ist. Genauso war´s
bei der 220. 220 ist nämlich durch 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 und
110 teilbar."
"Und warum haben die dann gewechselt?"
„Wenn du die Teiler der einen Zahl zusammenzählst, kommt gerade die andere Zahl heraus. Und deswegen waren die Araber befreundet. Zwei Zahlen bei denen die Summe der echten Teiler gerade die jeweils andere ist, heißen befreundete Zahlen."
Max überlegte, ob es bei Menschen wohl genauso leicht herauszufinden war,
ob zwei miteinander befreundet sind. Aber ihm fiel nichts ein, was dafür
geeignet wäre.
"Hey, du hörst mir ja gar nicht zu. Ich habe dir gerade von vollkommenen
Zahlen erzählt", unterbrach Emmy seine Gedanken. "Vollkommene
Zahlen sind solche, die mit sich selbst befreundet sind."
"Naja, bei uns Menschen würde man das wohl eher als Einsiedler bezeichnen. Ich hab schon eine gefunden! Die 6! Sie ist durch 1, 2 und 3 teilbar. Und 1 plus 2 plus 3 ist wieder 6!"
"Genau, und die nächste ist 28. Du wirst noch zum Zahlentheoretiker."
"Und ich dachte, in der Zahlentheorie geht es um Primzahlen und den Satz von Fermat?"
"Geht es auch. Schau mal hier. Hier wird das mit den
Primzahlen
und hier das mit
mit Fermats letztem Satz
erklärt.
"Ich bin schläfrig, später", sagte Max und die beiden legten sich unter die Kastanie im Hof und machten ein kleines Nickerchen.
Anmerkung der Redaktion: Hier gibt es eine ausführliche Einführung in die Zahlentheorie.
Geh zum nächsten Artikel oder lies noch "Rund um Primzahlen" und "Fermats letzter Satz"
Gibt es unendlich viele Primzahlzwillinge?
Kann man jede gerade Zahl als Summe zweier Primzahlen darstellen?
Stopp – ganz langsam. Erinnern wir uns doch erstmal, was Primzahlen sind:
Primzahlen sind natürliche Zahlen, die nur durch sich selbst und durch 1 teilbar sind. Die 1 zählt dabei nicht. Beispiele? - Klar doch: 2,3,5,7,11,...,37,...,127,... Nehmen wir uns irgendeine natürliche Zahl, zum Beispiel die 132, und fangen an, sie in einzelne Faktoren (Faktor * Faktor = Produkt) aufzuspalten.
Erstmal sieht man ganz klar, dass sie durch 2 teilbar ist: 132=66*2. Die 2 ist eine Primzahl, die können wir nicht mehr zerhacken, aber die 66 geht. 132=33*2*2. Die 33 auch: 132=11*3*2*2. So, jetzt sind alles Primzahlen.
Diesen Vorgang nennt man dann "Zerlegung in Primfaktoren". Was schon das Beispiel vermuten lässt: Jede Zahl kann in Primfaktoren zerlegt werden, bei Primzahlen ist es einfach zum Beispiel 3=3.
Hört sich schwer an, ist es aber nicht. Stellen wir uns vor, wir haben
schon 4 aufeinander folgende Primzahlen gefunden also die 2,3,5 und die 7.
Jetzt multiplizieren wir die alle miteinander und addieren 1, raus kommt 211.
Das ist ebenfalls eine Primzahl. Wir haben also eine noch größere
Primzahl gefunden.
Hätten wir die ersten 6 Primzahlen, also 2, 3, 5, 7, 11, 13 genommen, so
wäre 30031 rausgekommen. Dies ist keine Primzahl, denn 30031=509*59. Sie
kann aber gar nicht durch 2,3,5,7,11 oder 13 teilbar sein, denn 30030 ist ja
schon durch alle diese Zahlen teilbar.
30031 muss also einen Primfaktor haben der größer ist als 13. Das stimmt auch, denn 59 ist eine Primzahl und größer als 13. Wir haben also wieder eine Primzahl gefunden, die größer ist als die ersten 6.
Wir hätten natürlich auch die ersten 37 oder die ersten 10647 Primzahlen
nehmen können - einer der beiden Fälle hätte eintreten müssen:
Entweder wäre - wie bei den ersten 4 Primzahlen - das Produkt+1 selbst
eine Primzahl gewesen, oder - wie bei den ersten 6 Primzahlen - müsste
es in dem Produkt+1 einen Primfaktor geben, der größer ist als die
bisher gefundenen.
Das heißt – egal wie weit man bei der Suche nach möglichst
großen Primzahlen fortgeschritten ist - es gibt immer noch eine größere,
und man wird nie fertig.
Anders gesagt: Es gibt unendlich viele Primzahlen! Na, war doch gar nicht schwer,
oder?
Gibt es unendlich viele Primzahlzwillinge?
Das ist viel schwieriger. Ehrlich gesagt, wir von Mathe-rockt! wissen es nicht, und es weiß auch niemand anderes. Also legt los, denkt darüber nach. Was sind denn das, Primzahlzwillinge?
Ganz einfach, Primzahlzwillinge sind 2 Primzahlen, die sich nur um 2 unterscheiden. Also 3 und 5; 5 und 7; 11 und 13; 71 und 73. Es sind noch viele, viele weitere bekannt, und es sind fast alle davon überzeugt, dass es unendlich viele gibt, aber zeigen konnte das bisher niemand.
Es ist übrigens sehr typisch für die Zahlentheorie, dass man ganz einfache Fragen stellen kann, die sehr schwer zu beantworten sind. Und eigentlich können alle mitmachen, weil kein großes Mathematikwissen nötig ist. Im Gegenteil, frisches unverbogenes Denken verhilft viel eher zum Sieg als ewige Paukerei.
Kann man jede gerade Zahl als Summe zweier Primzahlen darstellen?
Eine andere unbeantwortete Frage ist die Goldbachsche Vermutung. Goldbach (1690-1746) hat sie bereits 1742 formuliert, und sie ist bis heute weder gezeigt noch widerlegt.
Er hat behauptet, jede gerade Zahl ließe sich als Summe zweier Primzahlen darstellen. Das stimmt auch für alle, die man bisher untersucht hat (und große Computer können sehr schnell sehr viele Zahlen untersuchen!), Zum Beispiel 4=2+2; 6=3+3; 8=5+3; 10=5+5; 12=7+5 usw. Aber gilt es wirklich für alle?
Er ist bewiesen!
Der Satz des
Pythagoras
besagt, dass für die Seitenlängen a,b,c eines
rechtwinkligen Dreiecks gilt:  .
.
Das ist natürlich Geometrie, die Zahlentheoretiker fragen sich an der Stelle
nun, ob es ganzzahlige Lösungen gibt.
Sie fragen sich, ob es rechtwinklige Dreiecke mit nur ganzzahligen Seitenlängen
gibt.
Und die Antwort ist ja: Für ein Dreieck mit den Seitenlängen a=3,
b=4 und c=5 gilt
 .
.
Also ist es nach dem Satz
des Pythagoras rechtwinklig. Es lassen sich sogar unendlich viele solcher "pythagoräischen
Zahlentripel" finden, aber das ist zu lang für diesen Artikel.
Pierre de Fermat (1607/08 - 1665)
hat sich im 17. Jahrhundert gefragt, ob es auch ganzzahlige
Lösungen für die Gleichung 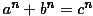 für Exponenten größer
als 2 gibt. Also zum Beispiel für die Gleichungen
für Exponenten größer
als 2 gibt. Also zum Beispiel für die Gleichungen  oder
oder
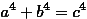 oder
oder 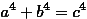 .
.
Fermat behauptete, dass es für keine solche Gleichung eine ganzzahlige
Lösung gibt (außer, wenn die 2 oben steht). Und er hat in seinem Notizbuch
am Rande vermerkt, dass er dafür einen gar wunderbaren Beweis gefunden habe,
der aber zu lang ist für diesen Rand.
Tja, und als nach Fermats Tod das Notizbuch veröffentlicht wurde, ging
das große Rätseln los. Tausende Mathematiker haben sich an dem Problem
die Zähne ausgebissen, selbst ein hohes Preisgeld, das zum Lösen
anspornen sollte, half nichts.
Fermats letzter Satz ist auch so eine Frage, die sich ganz einfach stellen
lässt, deren Antwort aber wahres Genie bedarf.
1993 – oder besser 1994, denn im ursprünglichen Beweis war noch eine
Lücke – hat Andrew Wiles die harte Nuss geknackt. Zwar hat Andrew
mit Sicherheit nicht Fermats eleganten Beweis gefunden, denn er hat gegen die
einfache Frage schwere Geschütze der modernen Mathematik ins Feld geführt,
aber immerhin hat er nach mehr als 300 Jahren einen Beweis gefunden.
Und es ist amtlich: Die Gleichung 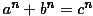 hat nur ganzzahlige Lösungen
a,b,c, wenn n gleich zwei ist.
hat nur ganzzahlige Lösungen
a,b,c, wenn n gleich zwei ist.