ALGEBRA
bei matherockt.de

Etta Zuber Falconer . Evariste Galois . Hypatia . Mary Somerville . Nicolas Bourbaki . Omar Khayyam . Seki Takakazu . Therese Hance

Emmy stieß eine schwere Eichentür erwartungsvoll auf. Alles was sie sah, waren drei Porträts. Evariste, Therese und Hypatia stand auf den kleinen Schildchen daneben. Enttäuscht wollte sie schon wieder gehen, doch Max zeigte ihr den Durchgang am rechten Ende des schmalen Raumes. Dahinter tat sich ein Labyrinth von halbhohen Vitrinen, Schaukästen und Tischen auf. Gemeinsam liefen sie durch die Gänge, bis Max vor einem Tisch mit lauter Schrauben stehen blieb

"Vektoren sind vorstellbar als gerichtete Größen im Raum", war der einzige Hinweis, der sich finden ließ. Max schaute Emmy fragend an.
"Du kannst dir Vektoren als Stöcke mit Spitzen dran vorstellen. Sie zeigen in eine Richtung und ihre Länge gibt an, mit welcher Kraft sie zeigen."
"Und wozu sind sie gut?"

"Nun, sie sind sozusagen die 'Zahlen' der Geometrie. Alles was man in der Geometrie wissen will, kann man mit ihnen ausrechnen. Flächeninhalte, Schwerpunkte, alles was sonst mühsam zeichnerisch herausgefunden werden muss."
Max war von Stöcken mit Spitzen nicht sehr begeistert und zeigte auf ein Plakat gegenüber. "Schau mal! Das hat aber nichts mit Geometrie zu tun?"

"Aber mit Vektoren. Zahlen, die mehrere Gleichungen gleichzeitig erfüllen, kann man mit Vektoren finden. Das gibt es ganz oft: Zwei Fragen, die erstmal nichts miteinander zu tun haben, können mit den gleichen Mitteln beantwortet werden."
Max hätte gern noch mehr gehört, aber ein Banner zwei Ecken weiter lenkte ihn ab.

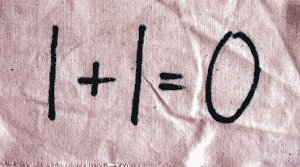
"1+1=0. Das ist doch Quatsch!"
"Oh, das sieht nach Gruppentheorie aus. Hier ist nur der Rest beim Teilen durch zwei wichtig. Eins plus Eins lässt beim Teilen durch zwei den Rest Null."

"Aha, dann ist also 1+1+1=1, weil 1+1+1 in normalen Zahlen drei ist, und drei beim Teilen durch zwei den Rest eins lässt?"
"Ja. In der Gruppentheorie sind die konkreten Zahlen gar nicht wesentlich. Wichtig ist nur, in welcher Beziehung sie zueinander stehen. Es geht sowieso selten um Zahlen. Guck mal hier siehst du die Symmetriegruppe des Lo Shu." Max las die Erklärung zu dem Bild voller magischer Quadrate.

Währenddessen betrachtete Emmy eine Vitrine mit einer DVD, einer Kreditkarte, von Saftpackungen abgerissenen Barcodes und anderem Alltagskram.

Sie geriet mal wieder ins Staunen, wozu so etwas abgehobenes, weltfremdes wie die Algebra gut sein kann - bei jeder DVD braucht man sie, um die Informationen abzuspeichern und wieder auszulesen. Und wie gut, dass die Algebra sogar erlaubt festzustellen, wo Fehler gemacht wurden und sie automatisch zu korrigieren! Sonst würde jeder Minikratzer den Film ruckeln lassen.
Max riss sie aus ihren Gedanken, steckt ihr einen Flyer über Galois-Theorie zu und zog Emma zum nächsten Raum.

Symmetriegruppe des Lo Shu
Das Lo Shu kennen alle, die die Mathe-Rockt-Galerie betreten haben:

Was gibt es noch für magische Quadrate?
Man kann es sich einfach machen und das Lo Shu drehen oder spiegeln. Dabei entsteht auf jeden Fall wieder ein magisches Quadrat, denn die Summe einer Reihe oder Diagonale ändert sich nicht.

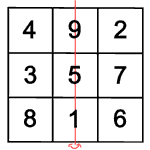
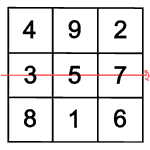
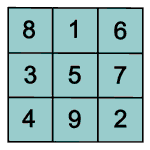
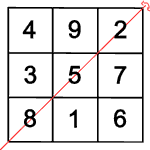
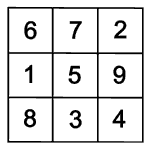
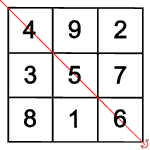
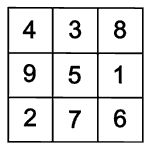
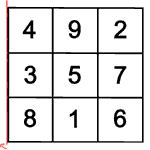
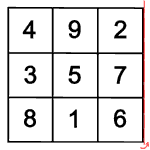
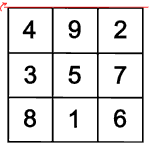
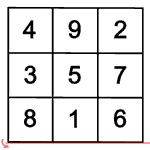
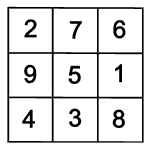
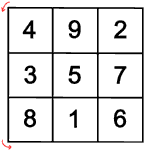
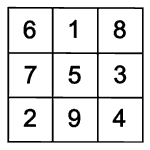
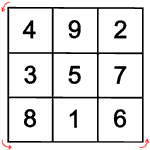
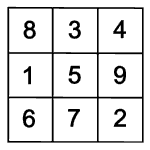
Einige der gedrehten und gespiegelten magischen Quadrate sind gleich, es kommen nur acht verschiedene heraus.

Wenn man eins von diesen acht Quadraten weiter dreht oder spiegelt, entsteht wieder eins von den schon bekannten acht Quadraten. Alle Bewegungen, die unterschiedliche magische Quadrate ergeben, heißen Symmetriegruppe.

Die Algebra hat Möglichkeiten gefunden, in Gruppen genauso zu rechnen wie mit Zahlen. Das klingt erstmal absurd, aber mit Evaristes Galois-Theorie kann man mit Gruppen uralte Fragen beantworten.

Übrigens: wer mehr über die Symmetrien des Lo Shu wissen will, kann hier weiterlesen: magic-squares.de

Galois-Theorie
Wir wollen hier ein paar der abstrakten Strukturen der Algebra andeuten, erklären welche grundsätzlichen Ideen Galois hatte und welche ungeahnten Anwendungsmöglichkeiten sich ergeben.

Fangen wir mit Gruppen an. Eine Gruppe ist eine Menge von Objekten, und eine Operation, die sich zwei Objekte nimmt und ein drittes ausspuckt. Das Ganze funktioniert so, wie wenn man ganze Zahlen addiert. Wichtig ist, dass es so etwas wie die 0 gibt, die bei der Addition ja nichts ändert. Und dass es sowas wie "Minus" gibt, also dass man zu jedem Objekt ein anderes finden kann, so dass sie zusammen "0" ergeben.

Die Objekte der Gruppe können Zahlen sein, müssen aber nicht. Sie können zum Beispiel auch die Symmetrien eines magischen Quadrats sein. Also alle Bewegungen, die man mit dem magischen Quadrat machen kann, so dass wieder ein magisches Quadrat herauskommt. Die Operation ist dann einfach das Nacheinander-Ausführen solcher Bewegungen. Aber Achtung: Dabei kann es durchaus wichtig sein, in welcher Reihenfolge man die Bewegungen ausführt!

Gibt es nun eine weitere Operation, und funktioniert alles wie bei den rationalen Zahlen mit der Addition und der Multiplikation, dann heißt die Menge mit den beiden Operationen "Körper". Man kann zu einem Körper mehr Objekte dazunehmen, wobei man natürlich erklären muss, wie die Operationen mit diesen Objekten funktionieren. Kommt dabei wieder ein Körper raus, so heißt dieser Körpererweiterung.

Zum Beispiel kann man zu den rationalen Zahlen alle Zahlen dazunehmen, die folgendermaßen aussehen (a und b sind rationale Zahlen): a+b*√2. Damit hat man wieder einen Körper, gerechnet wird genauso, wie in den reellen Zahlen.

Stellen wir uns jetzt eine Blackbox vor, die ein Element aus der Körpererweiterung nimmt und auf der anderen Seite wieder ein Element der Körpererweiterung ausspuckt. Das ausgespuckte Element muss natürlich nicht gleich dem genommenen sein. Eine "gute Blackbox" ist eine, die so arbeitet, dass es egal ist, ob ich zwei Elemente erst jedes für sich durch die Blackbox schicke und hinterher eine der Operationen ausführe, oder ob ich sie erst eine Operation ausführe und dann das Ergebnis durch die Blackbox schicke. Eine "sehr gute" Blackbox ist eine gute Blackbox, die, wenn sie ein Element des ursprünglichen Körpers (also der, der erweitert worden ist) nimmt, dasselbe Element wieder ausspuckt.

Habe ich einen Körper mitsamt einer Körpererweiterung vorgegeben, dann ist die Menge aller vorstellbaren "sehr guten" Blackboxen eine Gruppe, nämlich die Galois-Gruppe der Körpererweiterung.

Jetzt zu der berechtigten Frage, was das alles soll.

Erstmal eine antike Legende: 430 v. Chr. gab es auf der Insel Delos eine Pestepidemie. Die Bewohner haben das Orakel von Delphi um Rat gefragt. Sie bekamen die Aufgabe den Altar im Tempel des Apollon zu verdoppeln. Der Altar war ein Würfel und die antiken Mathematiker haben die Aufgabe so verstanden, dass sie nur mit dem Zirkel und einem Lineal ohne cm-Einteilung einen Würfel mit doppeltem Volumen konstruieren sollten.

An dieser Aufgabe haben sich viele Leute die Zähne ausgebissen. Im 19. Jahrhundert konnte man dann mit Hilfe der Galois-Theorie beweisen, dass diese Aufgabe gar nicht lösbar ist!

Eine andere klassische Aufgabe ist die, zu einem gegebenen Kreis wieder nur mit Zirkel und einem unmarkierten Lineal ein Quadrat mit gleichem Flächeninhalt zu konstruieren, die sogenannte "Quadratur des Kreises".

Auch diese Aufgabe ist nicht lösbar, und um das zu zeigen, braucht man wieder Galois-Theorie. Genauso verhält es sich mit der Aufgabe, einen Winkel nur mit Zirkel und Lineal zu dritteln.

Es gibt aber auch nicht-geometrische Fragen, die man mit Galois-Theorie beantworten kann. Für quadratische Gleichungen gibt es ja eine Lösungsformel, die sogar recht einfach ist - die pq-Formel. Auch für kubische Gleichungen und Gleichungen vierten Grades gibt es Lösungsformeln, die allerdings viel komplizierter sind. Aber das ist für Mathematiker egal, Hauptsache es gibt eine Formel!

Wenn man einen Computer benutzt, ist es egal, wie kompliziert die Formel ist, der kann viel schneller rechnen als wir. Für Gleichungen fünften Grades oder noch höheren Potenzen, konnte man aber keine Formel finden. Und auch hier kann man mit der Galois-Theorie zeigen, dass es eine solche Formel gar nicht geben kann!

Bei all diesen Problemen ist erstaunlich, dass unsere Unkenntnis einer Lösung nicht daran liegt, dass wir zu dumm sind, sondern dass es einfach keine Lösung geben kann. Und dass man das auch noch beweisen kann, ist noch erstaunlicher.

Zum Schluss wollen wir noch zeigen, was die Galois-Gruppe mit der Würfelverdoppelung zu tun hat. Anfangs kennt man also nur die Seitenlänge des Ausgangswürfels, sagen wir der Einfachheit halber, sie ist 1. Die Zahlen 2, 3 und so weiter können ganz einfach konstruiert werden. Damit bekommt man so etwas wie einen Zahlenstrahl mit den ganzen Zahlen markiert.

Es ist auch nicht schwer ½, ¼ usw. zu konstruieren. Damit kann jede beliebige rationale Zahl auf dem Zahlenstrahl markiert werden. Jetzt haben wir immerhin schon einen Körper, den wir kennen.

Durch geschicktes Weiterkonstruieren bekommen wir viele weitere Zahlen (zum Beispiel √2, indem wir die Diagonale eines Quadrats der Seitenlänge 1 abtragen). Wir können die rationalen Zahlen also Stück für Stück um "konstruierbare" Zahlen erweitern. Alle konstruierbaren Zahlen bilden eine Körpererweiterung.

Erweitert man die rationalen Zahlen um eine einzige konstruierbare Zahl, dann hat die Galois-Gruppe davon eine gerade Anzahl von Elementen.

Ein Würfel der Seitenlänge 2^(1/3) hat gerade das doppelte Volumen eines Würfels der Seitenlänge 1. Die Aufgabe ist also gelöst, wenn wir die Zahl 2^(1/3) konstruiert haben. Und andersrum: Wenn wir die Aufgabe gelöst haben, haben wir die Zahl 2^(1/3) konstruiert. Das heißt: Die Aufgabe ist genau dann lösbar, wenn 2^(1/3) eine konstruierbare Zahl ist.

Erweitert man die rationalen Zahlen aber um 2^(1/3), dann hat die Galois-Gruppe 3 Elemente. Deshalb kann also 2^(1/3) keine konstruierbare Zahl sein und jegliche Versuche zu einem gegebenen Würfel einen Würfel mit doppeltem Volumen nur mit Zirkel und Lineal zu konstruieren müssen scheitern.
Wer das genauer wissen will, der kann auf http://www.galois-theorie.de/ weiterlesen. Dort ist eine detailliertere Einführung in die Galois-Theorie dargestellt, die erklärt, warum es keine Lösungsformeln für Gleichungen fünften Grades geben kann.

Und wer's noch mathematischer mag, der kann http://nrich.maths.org/ lesen. Der Artikel ist auf Englisch und führt in einer sehr mathematischen Sprache, die aber für Interessierte durchaus verständlich ist, in die Konzepte der Galois-Theorie ein.

Und wer eine fundierte, locker geschriebene Einführung in die Gruppentheorie sucht, die durchaus auch für Studienanfänger geeignet ist, der wird auf http://matheplanet.com/ fündig.

nach oben